拉扎维《模拟CMOS集成电路设计》第二版学习笔记
一、综述
1.1 MOS 结构
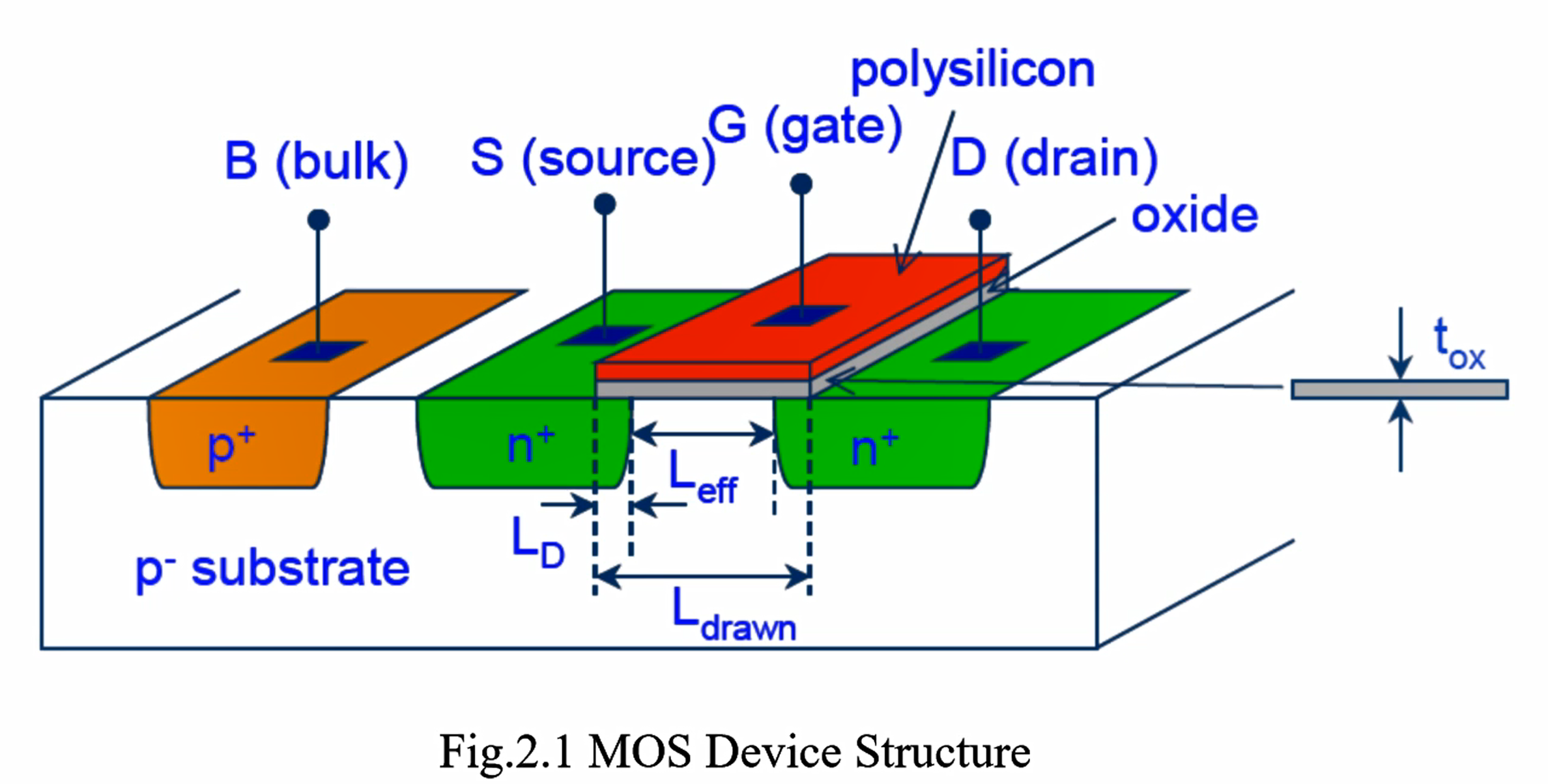
图解:
- n+ 指 n 型重掺杂;p- 指 p 型轻掺杂;
- polysilicon 为多晶硅,简写为 poly,用作导体;oxide 为栅氧化层,材料为 SiO2;
- 由于源极和漏极在注入时会发生横向扩散,沟道长 Leff 会略小于栅氧化层长度 Ldrawn;在之后的公式中,如未说明,L 指的都是 Leff;
- B(bulk) 端提供衬底电压;对于 NMOS 来说,由于源、漏极和衬底之间各自形成了一个从衬底指向源/漏极的二极管,为了避免导通时电流从这两个二极管漏出而并没有走沟道,我们往往需要将衬底接到最低电位来保证两个二极管是维持反偏的。同理,PMOS 需要将其衬底接在最高电位;
1.2 bulk 和阱
当需要在 p- 衬底上搭建 PMOS 的时候,就需要开辟一片 “n 阱”
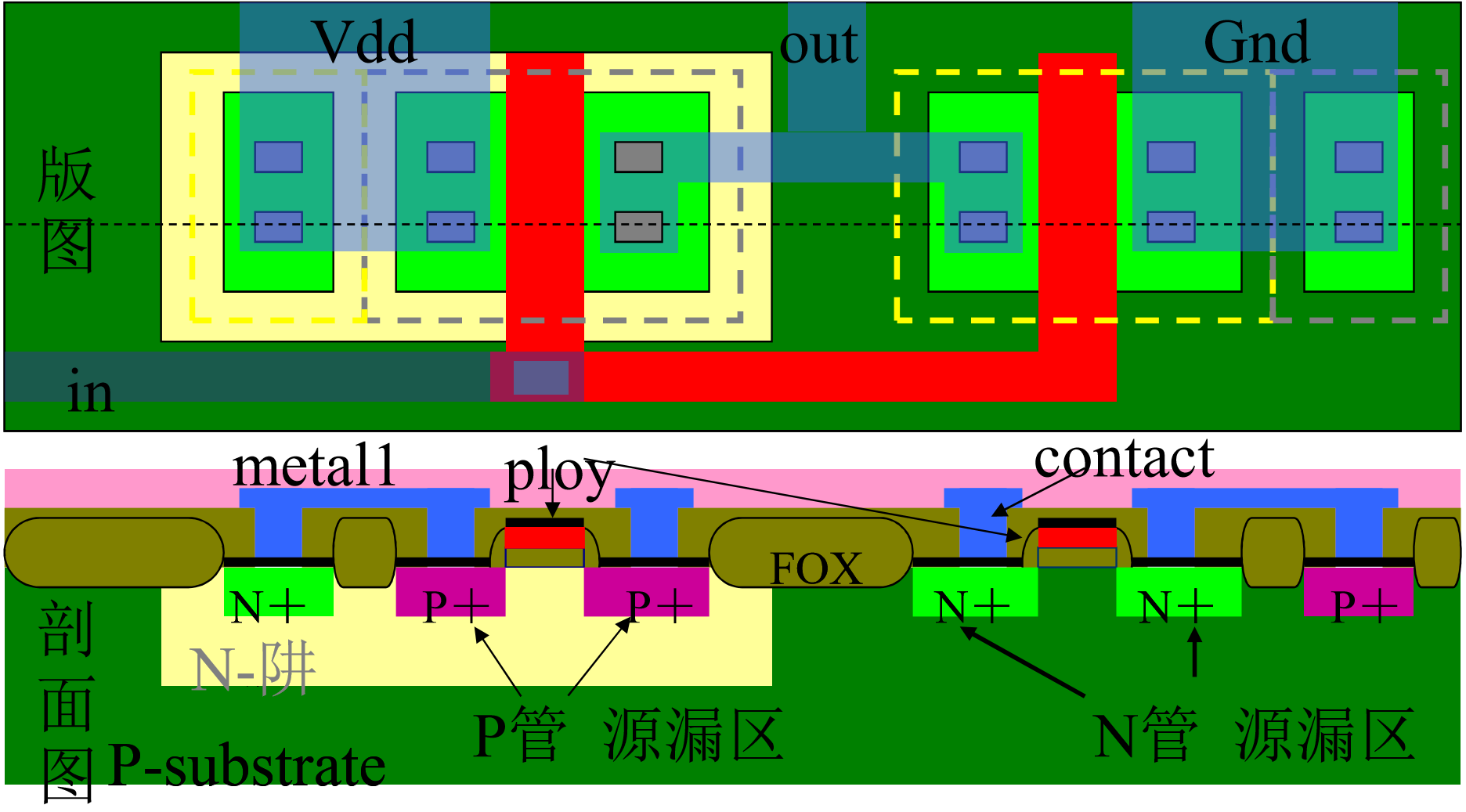
每一个引出的 bulk 端都只能控制其所在区域的衬底电压,如 n 阱中引出的 bulk 端只能控制此 n 阱的衬底电压,而从 p- 衬底引出的 bulk 端控制的则是整个 p- 衬底的电压。如果需要单独控制某些 NMOS 的衬底电压,让其不受其他 NMOS 衬底电压的影响,就需要引入“深 n 阱”——在 p- 衬底上先构建 n 阱,再在此 n 阱的基础上构建 p 阱,此 p 阱的衬底电压便独立于全局 p- 衬底电压之外。
- 为什么需要单独引出 B 端而非将衬底直接接地?
因为当前的工艺是平面工艺,衬底是无法直接接到地的。 - 为什么用 p+ 作为 B 端?
因为 p- 无法提供欧姆接触,而 p+ 可以。
1.3 MOS I/V 特性 (大信号)
1.3.1 沟道形成的过程
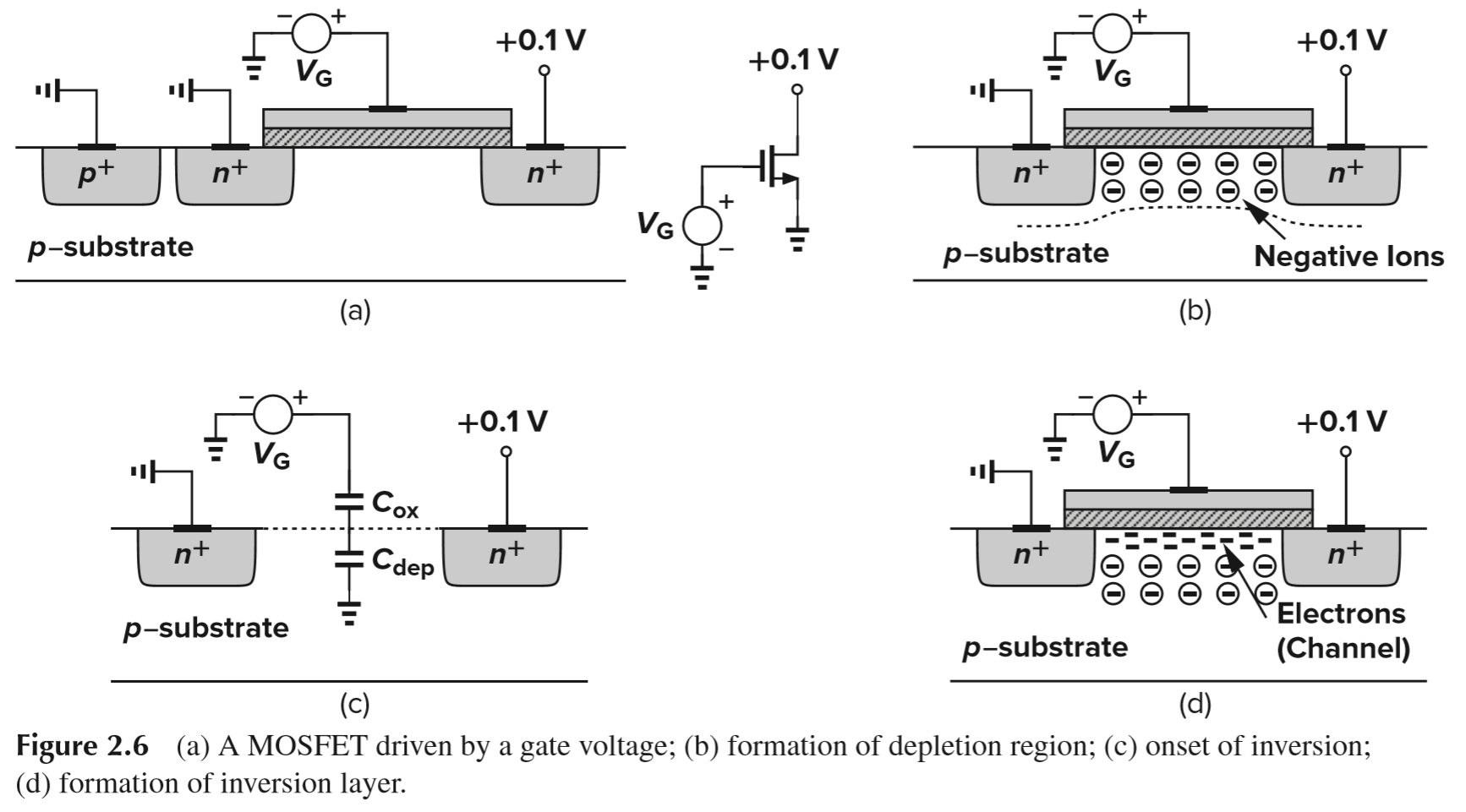
- Vg 从 0V 升高,将空穴赶离空间电荷区,留下负离子来镜像栅极正电荷,形成耗尽层 (图 b 箭头所指即为耗尽层);
- Vg 继续升高,耗尽层变厚,栅极到地相当于串联了两个电容:栅氧化层电容 Cox 和耗尽层电容 Cdep;
- Vg 到达 Vth 时,耗尽层负离子无以镜像栅极正电荷;且随 Vg 的升高,SiO2 和 p- 衬底间的界面电位升高,相当于给源、漏极的 PN 结加上了正偏电压,使得大量的电子从源、漏极扩散出来,与衬底被吸引上来的少量电子一起形成了导电沟道,即反型层;Vov = Vgs - Vth 称“过驱动量”,它是反型层产生的原因。
- 随着 Vg 的升高,沟道电子密度增加,若在漏源之间加正偏电压,产生的电流也会增加 (以上过程均是在 NMOS 的截止区和线性区);
注1:上面提到的 Cox 在后面的公式中,表示的是单位面积的栅氧化层电容而不是整个栅氧化层电容。
注2:Cox 和 tox 成反比,且当 tox = 20 Å (Å 读作“埃”,为 10 的 -10 次方米) 时,Cox = 17.25 fF/μm^2 。
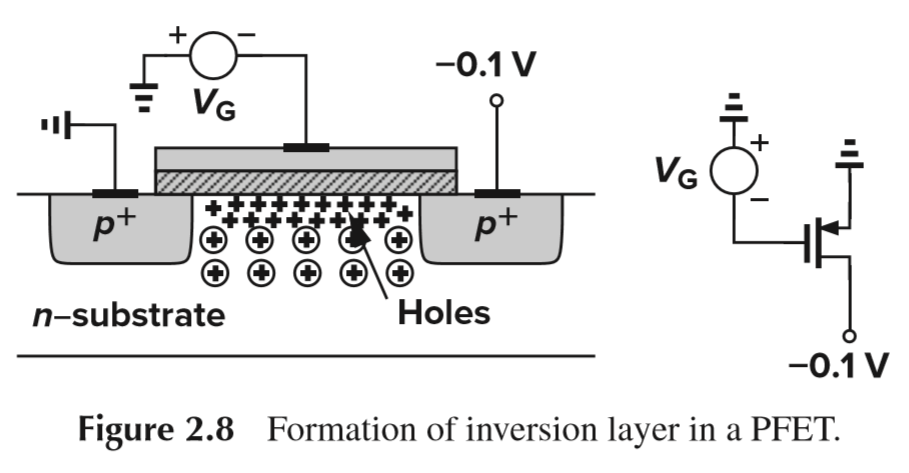
注3:对于 PMOS,只要将其所有的电源和电性都取反,即可:
1.3.2 I/V 特性的推导
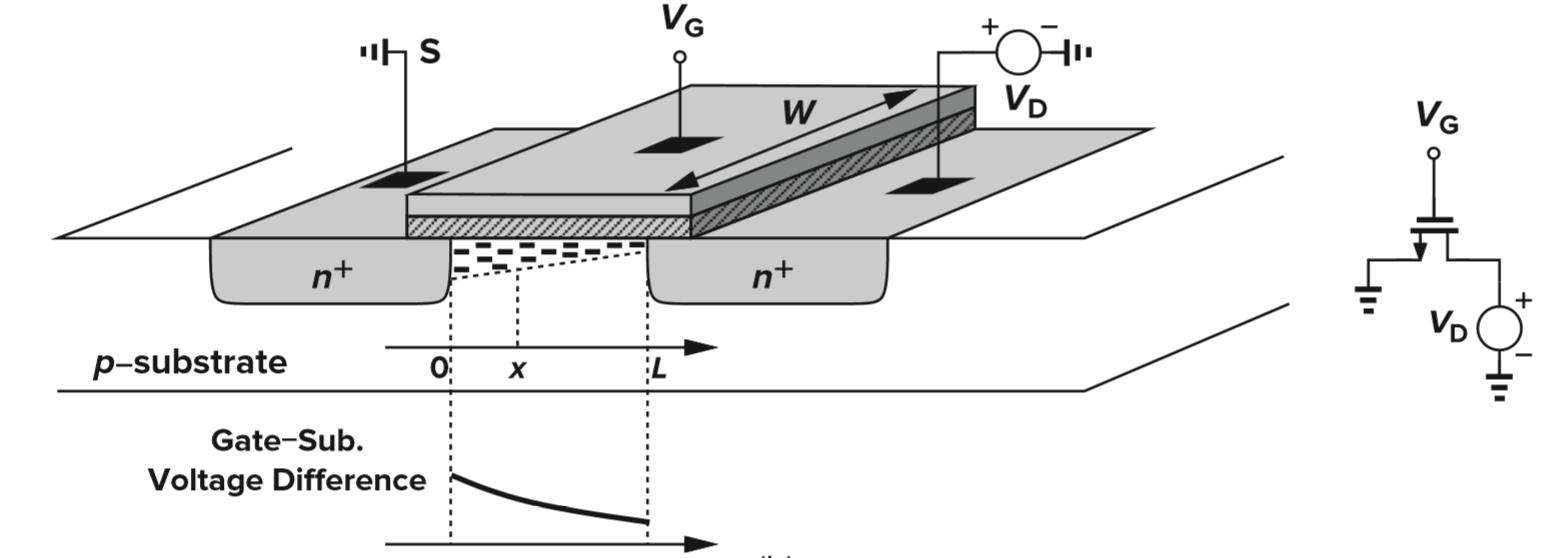
$$
先求单位长度的总电荷量:设V(x)为x处沟道电压,由于载流子为电子、需要加负号,故有:
$$
$$
Q_d = - WC_{ox}[V_{GS}-V(x)-T_{TH}]
$$
$$
再求x处沟道电流:I_D=Q_d\cdot v=-WC_{ox}[V_{GS}-V(x)-V_{TH}]\cdot v
$$
$$
代入v=\mu_n E,E=-{dv \over dx},有:I_D=WC_{ox}[V_{GS}-V(x)-V_{TH}]\mu_n{dV(x)\over dx}
$$
1、对于线性区 (三极管区),将 dx 从等式右边移到左边,左边在 [x=0,x=L] 范围积分、右边在 [V(x)=0,V(x)=Vds] 积分,可得:
$$
I_D=\mu_nC_{ox}{W\over L}[(V_{GS}-V_{TH})V_{DS}-{1\over 2}V_{DS}^2],\mathbb{V_{DS}<V_{GS}-V_{TH}}
$$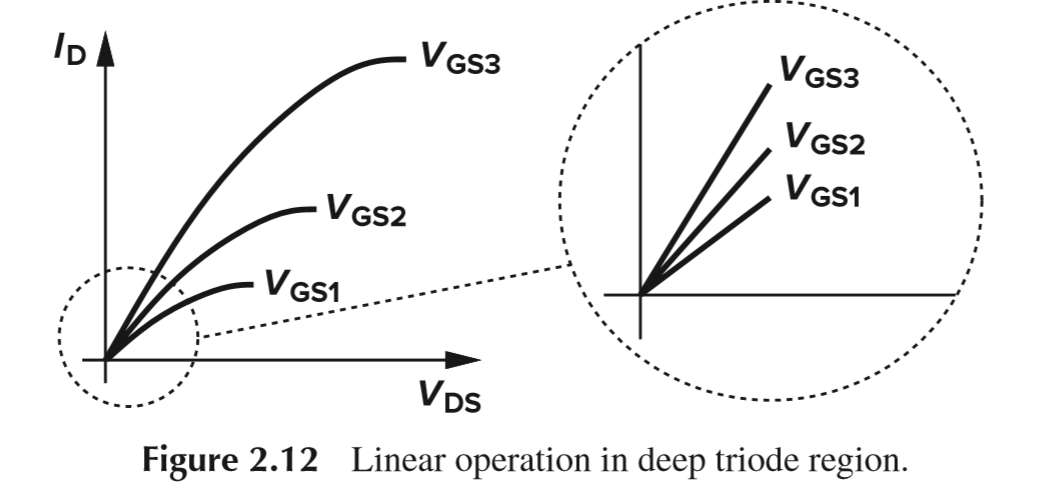
当 Vds 远小于 2(Vgs - Vth) 时,称作深线性区,此时可以忽略 Id 式子中 Vds 的平方项,即:
$$
I_D 与 V_{DS}成近似线性的关系:I_D=\mu_nC_{ox}{W\over L}(V_{GS}-V_{TH})V_{DS}
$$
$$
此时,沟道可近似看作一个电阻,阻值为:R_{on}={V_{DS}\over I_D}={1\over \mu_nC_{ox}{W\over L}(V_{GS}-V_{TH})}
$$
2、对于饱和区,沟道在 L’ 处夹断;只要左边在 [x=0, x=L’] 范围积分、右边在 [V(x)=0, V(x)=Vgs-Vth] 积分,可得:
$$
I_D={1\over 2}\mu_nC_{ox}{W\over L’}(V_{GS}-V_{TH})^2\approx{1\over2}\mu_nC_{ox}{W\over L}(V_{GS}-V_{TH})^2,\mathbb{V_{DS}\ge V_{GS}-V_{TH}}
$$
在 L 很长时,由于 L’ 很接近 L,这里将 Id 近似于沟道刚好夹断时的漏源电流,称为长沟近似。在长沟近似下,漏电流可视为不受到 Vds 影响。
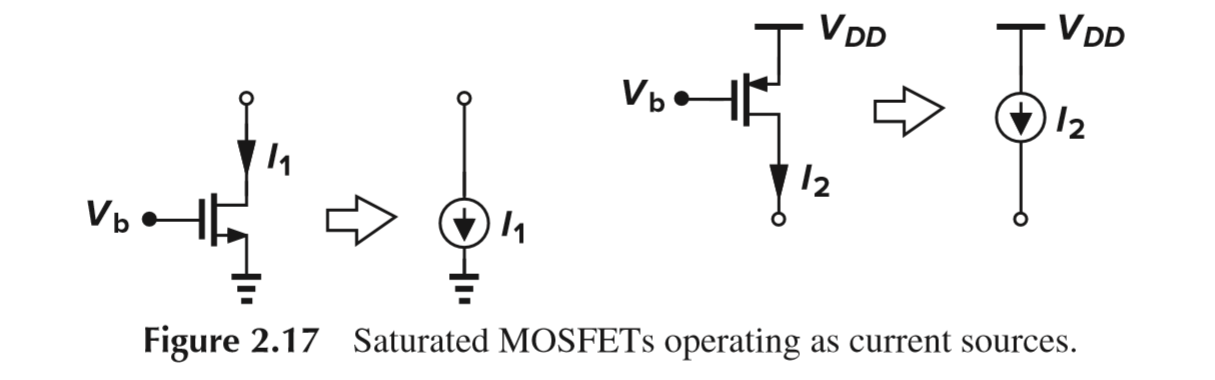
在饱和区工作的 MOS 管,可以视作电压控制的电流源。注意 NMOS 电流源是向地注入电流,而 PMOS 电流源是从 Vdd 抽取电流,即:每个电流源只有一个端点是“浮动”的;当需要 MOS 管工作在饱和区时,需要 Vds 大于 Vov,即 Vov 影响了输入信号的电压余度:Vov 越大,输入信号的电压余度越小。
注1:沟道夹断后,电子怎么移动到漏极?
在靠近沟道夹断点处,Qd 趋近于 0,而 v = I/Qd,故此时电子的速度很大,会将电子“发射”到漏极。
注2:PMOS 的 Vgs、Vds、Vth、Vgs - Vth 都是负数,且实际电流方向是从源极流向漏极;
注3:由于空穴迁移率低,所以 PMOS 的电流驱动能力也弱于 NMOS;
1.3.3 MOS 跨导
定义:用于表征 MOS 器件将电压转换为电流能力的品质因素;定义式如下:
$$
\begin{aligned}
g_m
&={\partial I_D \over \partial V_{GS}}\mid V_{DS}constant \
&=\mu_nC_{ox}{W\over L}(V_{GS}-V_{TH}) \
&=\sqrt{2\mu_nC_{ox}{W\over L}I_D} \
&={2I_D \over V_{GS}-V_{TH}} \
&={1\over R_{on}}
\end{aligned}
$$
在上述表达式中,Id 和 Vgs - Vth 都是偏置量;我们假定小信号引起这些偏置量的改变可以忽略。
上面的表达式指的是定义在饱和区的跨导;实际上器件工作在线性区时,也可以应用跨导这一概念。但是线性区的跨导比饱和区的更小,所以在放大应用时都会用饱和区的跨导;详见拉扎维书上例 2.3。
上面的表达式指的是 NMOS 的跨导,对于 PMOS,需要把上面所有包含 (Vgs - Vth) 的式子加个负号。
NMOS 跨导与各参量关系图如下:
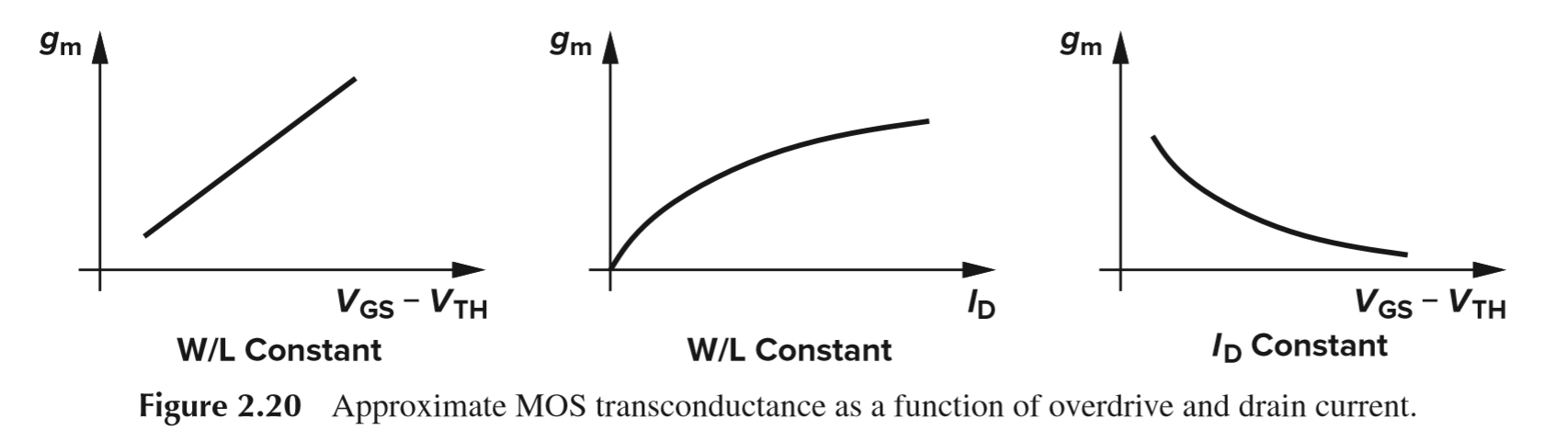
如果增加 W/L 但保持 Id 不变,跨导能否任意地增大?不能,详见书上的二级效应:亚阈值导电性。
1.4 二级效应
1.4.1 体效应
发生条件:源衬电压 Vsb > 0
结果:Vth 升高
$$
V_{TH}=V_{TH0}+\gamma(\sqrt{2\phi_F+V_{SB}}-\sqrt{|2\phi_F|})
$$
$$
其中,V_{TH0}=\phi_{MS}+2\phi_F+{Q_{dep}\over C_{ox}}
$$
反之,如果 Vsb 为负,Vth 也会下降。
1.4.2 沟道调制效应
发生条件:饱和区
原因:L’ 实际上是 Vds 的函数,令 ΔL = L - L’,ΔL/L = λVds (这只是近似线性,在短沟器件中这样的线性近似度会变得较低,见 17 章),则饱和区漏电流公式改为:
$$
I_D={1\over2}\mu_nC_{ox}{W\over L}(V_{GS}-V_{TH})^2(1+\lambda V_{DS})
$$
跨导 gm 的公式改为:
$$
\begin{aligned}
g_m
&={\partial I_D \over \partial V_{GS}}\mid V_{DS}constant \
&=\mu_nC_{ox}{W\over L}(V_{GS}-V_{TH})(1+\lambda V_{DS}) \
&=\sqrt{2\mu_nC_{ox}{W\over L}I_D(1+\lambda V_{DS})} \
&={2I_D \over V_{GS}-V_{TH}} \
&={1\over R_{on}}
\end{aligned}
$$
沟道越长,λ 越小。
需要注意的地方
- MOS 器件是一个对称的器件,它的源、漏极在物理层面上完全相同,只是连入电路之后扮演了不同的角色。因此我们也可以互换连接在源、漏极上的电路。换言之,电路图上标出的源极和漏极不一定是实际上的源极和漏极。
- PMOS 的 I/V 特性方程与 NMOS 的相同;书上加了负号,表明 Id 方向是从漏极流向源极;
- 线性区通常用作开关,饱和区通常用作放大器、电流源;
- Vs = 0、L’ = L 为一级近似,讨论二极效应就是为了去掉一级近似;