美赛准备(1)

数模美赛赛前准备——2020.10.1

一、绪论

1. 建议先写好中文，机器翻译后再人为修改。
2. 数据可以先准备好，配置好 vpn，再去美国的一些网站上找数据。实在不行可以自己造随机数。
3. 如果数据很庞大，可以先学一下数据库语言或者用 python 来处理，用 matlab 打开数据是很慢的。
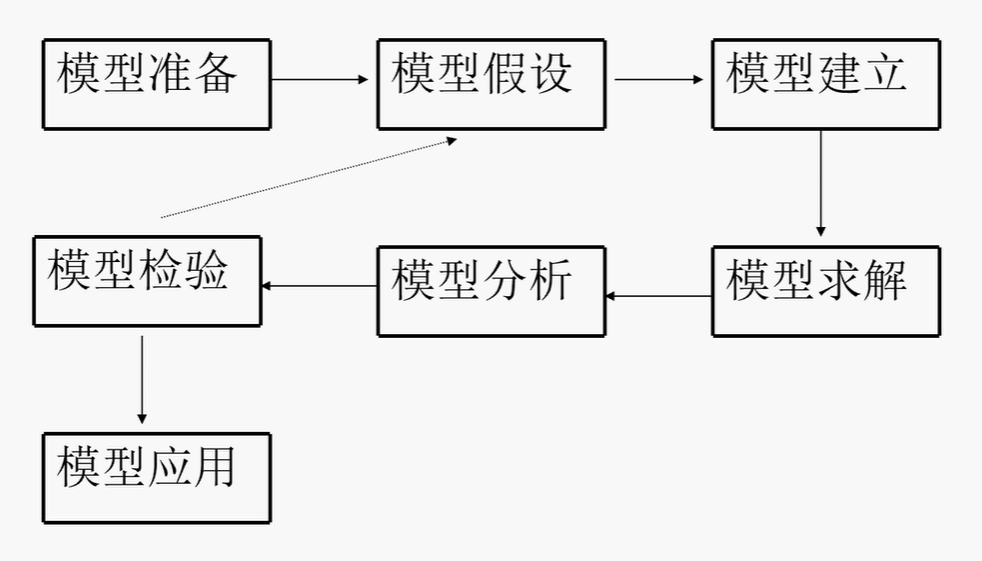
4. 论文至少包含问题分析、模型假设、模型建立、求解、结果分析等。
5. 组队分工：建模、编程(matlab)、论文。其中，论文写作不能完全交给一个人。
6. 赛题是什么类型？对应了哪一种模型？如何假设/简化？
7. 不能复制模型——可以尝试原创一些模型和算法，或者改进一些算法，或者组合创新(模型嵌套等)。
8. 数据里面可能有错误数据，需要剔除。模型求解的过程：先列数据、再对数据作预处理、再对模型建立的关键结果进行求解、最后才得到最终结果。
9. 结果分析：表层+深层 (表层：看图说话；深层：挖掘出内含的信息)
10. 模型检验、应用 (是否有可推广性、可改进性)

二、常见题型

2.1 数据处理问题

1. 插值拟合——主要用于对数据的补全和基本的趋势分析
2. 小波分析、聚类分析 (高斯混和聚类、K-均值聚类等)——主要用于诊断数据异常值并进行剔除
3. 主成分分析、线性判别分析、局部保留投影等——主要用于多维数据的降维处理、减少数据冗余
4. 均值、方差分析、协方差分析等统计方法——主要用于数据的截取或者特征选择

2.2 关联与因果问题

1. 灰色关联分析方法 (样本点个数较少)——经常使用！！
2. Superman 或 kendall 等级相关分析
3. Person 相关分析 (样本点个数较多)
4. Copula 相关分析 (金融数学、概率密度)
5. 典型相关分析 (适合于两组指标之间，或者若干指标与某一个指标之间的关系)——经常使用！！

2.3 分类与判别

2.3.1 分类

1. 距离聚类 (常见于坐标形式的数据，如城市划分等)——常用！！
2. 关联性聚类 (适用于挖掘各种指标之间的关联性)——常用！！
3. 层次聚类
4. 密度聚类
5. 其他聚类

2.3.2 判别

1. 贝叶斯判别 (统计判别方法)
2. 费舍尔判别 (训练的样本比较少)
3. 模糊识别 (分好类的数据点比较少)

2.4 评价与决策

1. 模糊综合评判 (主观性强，评价对象没有名确的指标、没有定量化的描述，仅对对象进行优良中差等层次评价，不可排序)
2. 主成分分析 (评价多个对象的水平并排序，指标间关联性很强)
3. 层次分析法 (需要通过指标综合考虑来做决策，主观性强，简单)
4. 数据包络(DEA)分析法 (适合经济方面的评价，如发展状况)
5. 秩和比综合评价法 (指标间关联性不强，不常用)
6. 神经网络评价 (多指标非线性关系名确的评价，需要大量数据)
7. 优劣解距离法 (TOPSIS法，主观性强)
8. 投影寻踪综合评价法 (糅合多种算法)
9. 方差分析、协方差分析 (较简单、低级，较少用)

2.5 预测与预报

2.5.1 试题类型

1. 小样本内部预测
2. 大样本内部预测
3. 小样本未来预测
4. 大样本未来预测
5. 大样本的随机因素或周期特征的未来预测

注：一般而言低于200个的数据样本数量都叫小样本。

2.5.2 适用模型

2.5.2.1 小样本未来预测

1. 灰色预测模型 (条件：数据样本点个数少，一般 0~50 个；且数据呈现指数或曲线的形式)——必须掌握！！
2. 微分方程预测 (适用于样本点数并不是很少，一般 50~100 个；且无法找到原始数据之间的关系，但可以找到原始数据变化素的之间的关系，通过公式推导转化为原始数据之间的关系)
3. 回归分析预测 (样本点个数一般 100~200 个，适用于求一个因变量与若干自变量之间的关系，若自变量变化之后，求因变量如何变化；且要求自变量之间协方差较小、关系小；样本点个数 n > 3k+1 ，k 为自变量个数；因变量要符合正态分布)——必须掌握！！

2.5.2.2 小样本内部预测

用插值拟合即可解决

2.5.2.3 大样本预测

1. 马尔科夫预测 (过去对未来没有影响，只有现在才对未来有影响；数据间随机性强且互不影响；序列之间无信息传递、前后无联系；只能得到概率)——备用
2. 时间预测序列 (ARMA 模型，周期模型，季节模型等，与马尔科夫预测互补)——必须掌握
3. 小波分析预测
4. 神经网络预测
5. 混沌序列预测

2.6 优化与控制

1. 线性规划、整数规划、0-1规划 (适用于较简单问题)
2. 非线性规划与智能优化算法 (适用于较复杂问题)
3. 图论、网络优化 (适用于多因素交错复杂)
4. 排队论与计算机仿真 (适合于过程性调度与控制)
5. 模糊规划
6. 灰色规划
7. 动态规划
8. 多目标规划和目标规划

赏

谢谢你请我吃小鱼干