美赛准备-2

2020-10-06
📖 阅读数: 次 |

📄 字数统计: 2.7k字 | ⏱ 阅读时长: 10分

数模美赛赛前准备——评价类问题

一、层次分析法

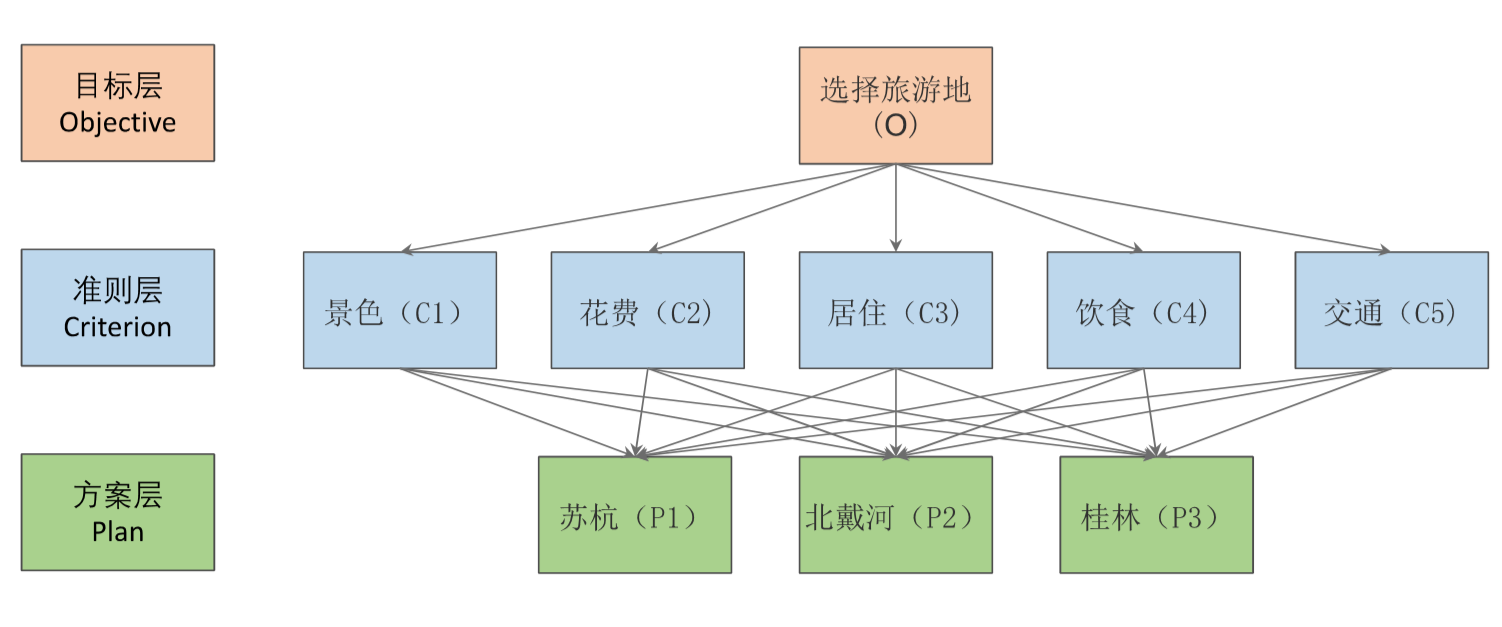
1.1 适用情况

指标未定——需要自己查询资料；
各指标所占权重未定——两两比较，得到判断矩阵；
指标的数量并不多(最多不得超过15个)；

1.2 详细步骤

1.2.1 确定指标（准则层）

查文献：知网、万方、百度/谷歌学术
搜索：虫部落
自己定

1.2.2 确定权重（准则层）

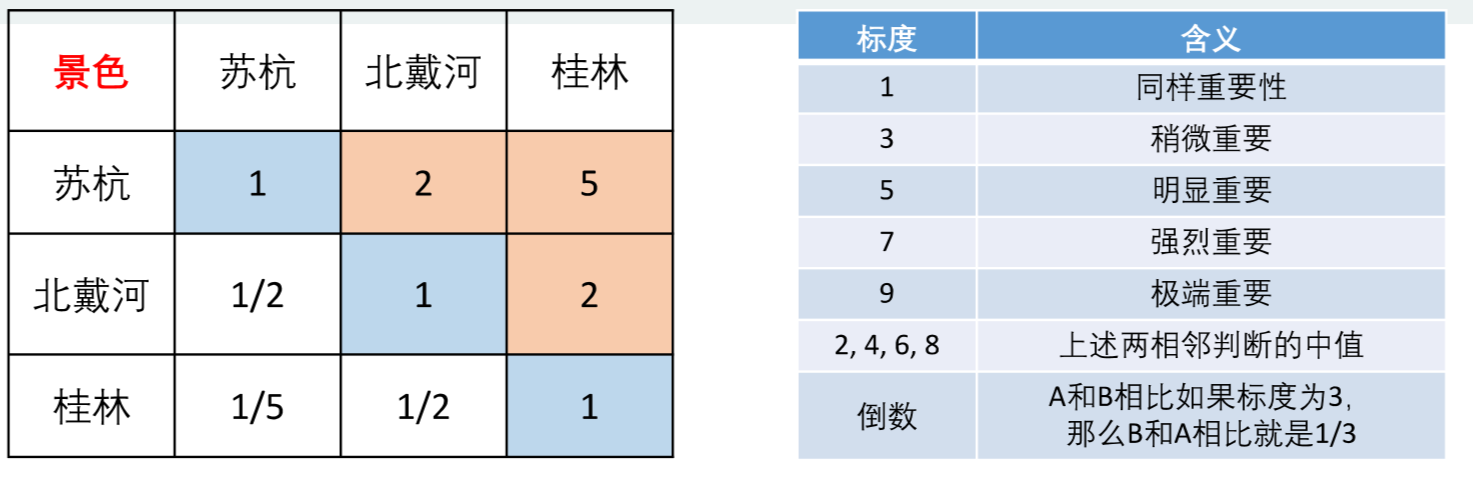
两两比较各指标对于最终评价目标的重要性：

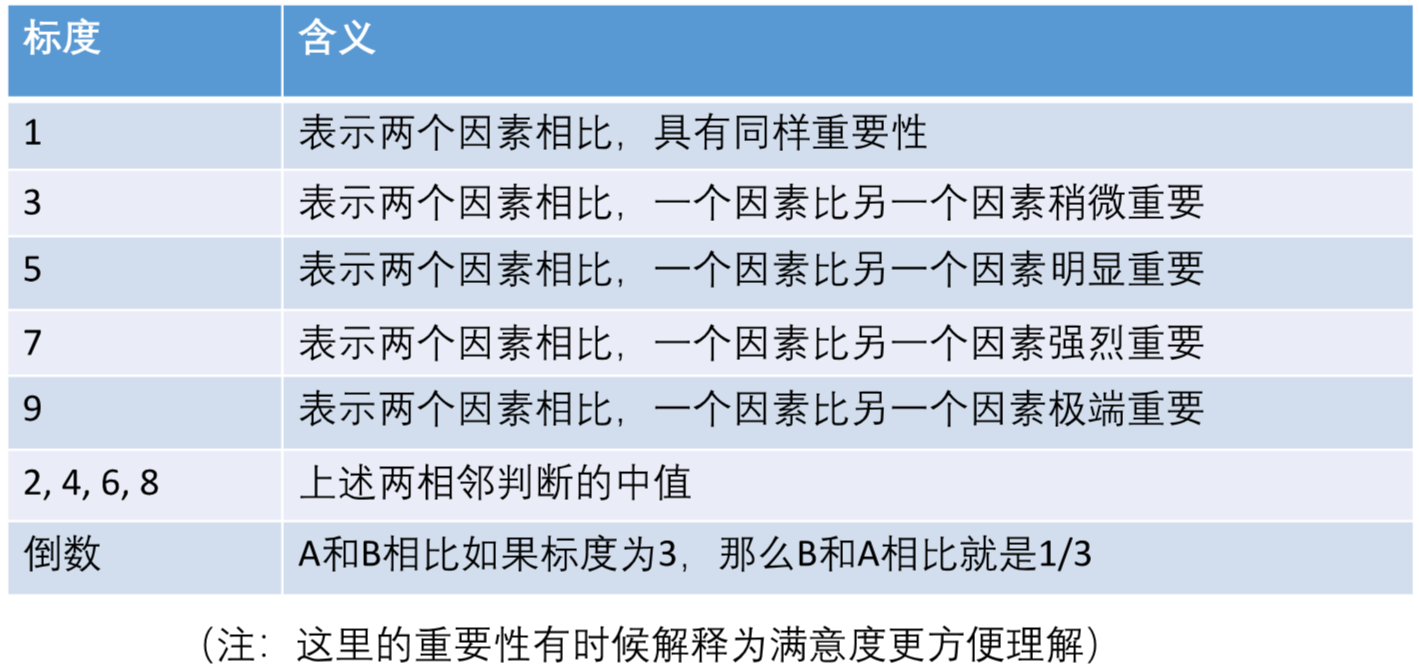
每进行一次比较，将标度值和它的倒数按照主对角线填入判断矩阵：

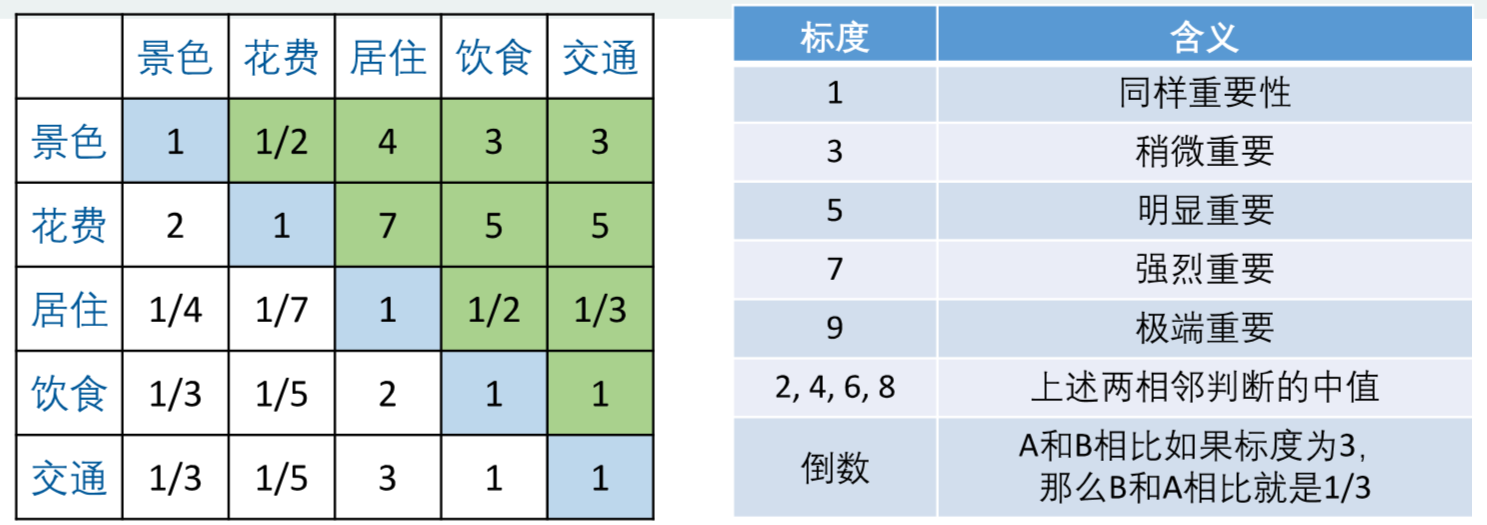
例：花费比景色重要，标度为2，则在（花费，景色）填2，（景色，花费）填1/2；

1.2.3 一致性检验（准则层）

一致矩阵的性质：各行成倍数关系；秩一定为1；有一个特征值为n (n为方阵的阶数，这里判断矩阵只可能为方阵)、其余特征值为0；且特征值n对应的特征向量刚好就是一致矩阵的第一列。

引理：n阶正互反矩阵A为一致矩阵时，当且仅当最大特征值 λmax=n；A非一致时，一定有 λmax>n；λmax为最大特征值。

一致性检验的步骤：

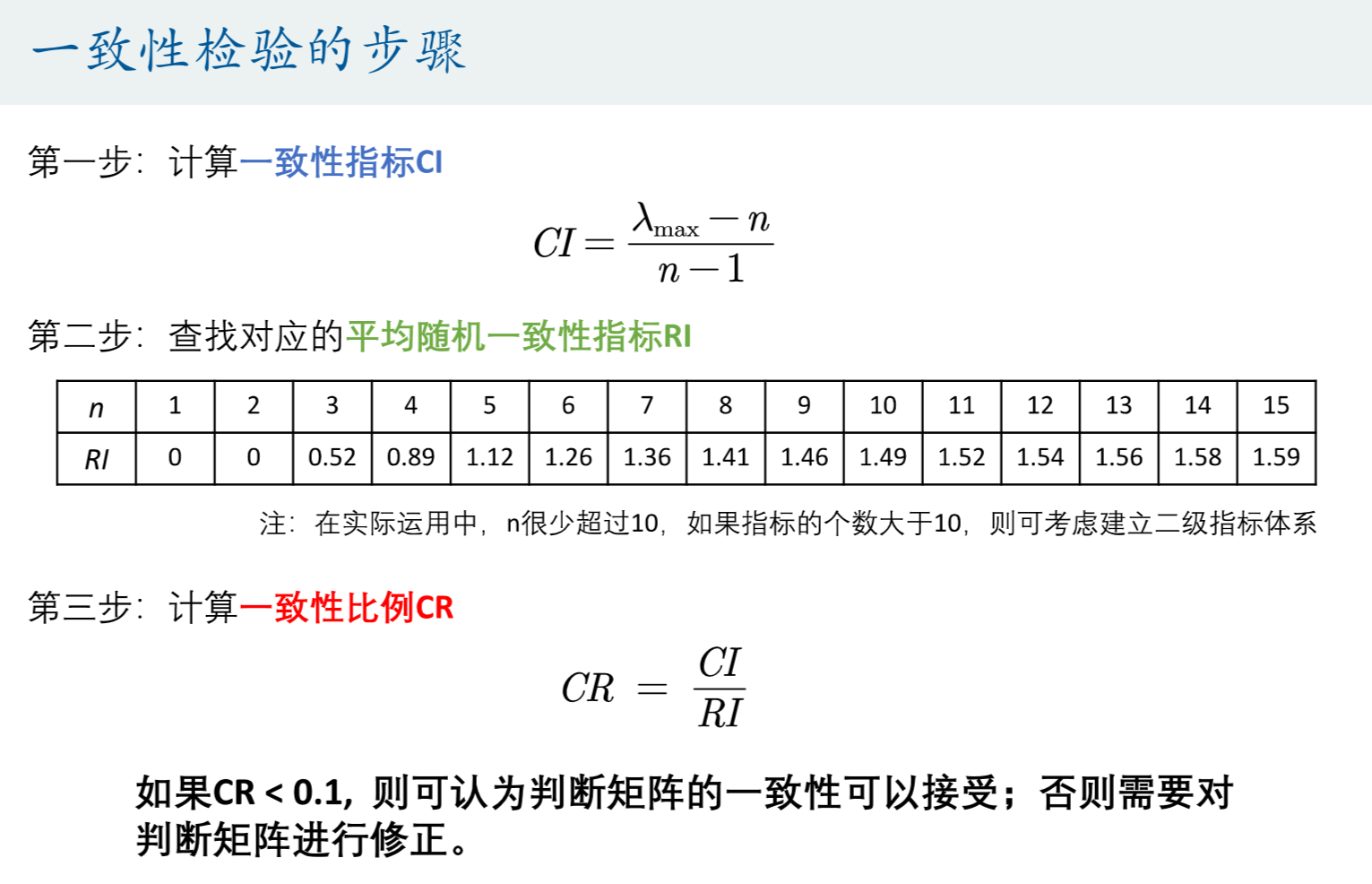
注：对非一致矩阵进行修正，只需要将其向各行成倍数的形式修改即可

主要代码：

[V,D] = eig(A);                 % 求矩阵A的全部特征值，构成对角阵D，并求A的特征向量构成V的列向量
Max_eig = max(max(D));          % 内部的max()是取出各列的最大值组成一个行向量；外部的max()是取出这个行向量中的最大值

CI = (Max_eig - n) / (n-1);
RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; 
% 这里n=2时，一定是一致矩阵，所以CI = 0，我们为了避免分母为0，将这里的第二个元素改为了很接近0的正数
CR=CI/RI(n);

if CR<0.10
    disp('因为CR<0.10，所以该判断矩阵A的一致性可以接受!');
else
    disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
end

1.2.4 计算权重（准则层）

1.2.4.1 算数平均法

%%%%%%%%%%%%%%%%%%%%% 将判断矩阵A归一化 %%%%%%%%%%%%%%%%%%%%%%%%%
Sum_A = sum(A);                        % 求各列所含元素的和，得到一个1行n列的行向量
SUM_A = repmat(Sum_A,n,1);			   % 将这个行向量在行方向复制并扩展成n行，列方向不变，形成n行n列的矩阵
Stand_A = A ./ SUM_A;				   % 将矩阵A中的各个元素除以矩阵SUM_A中的各个元素 (点除)

%%%%%%%%%%%%%%%%%%%%%% 算数平均法求权重 %%%%%%%%%%%%%%%%%%%%%%%%%
disp('算术平均法求权重的结果为：');
disp(sum(Stand_A,2)./n)                % 将归一化后的矩阵各行所含元素相加，得到n行1列的列向量；
									   % 再将此列向量中的各个元素除以n

1.2.4.2 几何平均法

Prduct_A = prod(A,2);                   % 求各行所含元素的和，得到一个n行1列的列向量
Prduct_n_A = Prduct_A .^ (1/n);         % 将此列向量的各个元素开n次方
disp('几何平均法求权重的结果为：');
disp(Prduct_n_A ./ sum(Prduct_n_A))     % 归一化

1.2.4.3 特征值法

[V,D] = eig(A);                         % 求矩阵A的全部特征值，构成对角阵D，并求A的特征向量构成V的列向量
Max_eig = max(max(D));                  % 求最大特征值
[r,c]=find(D == Max_eig , 1);           % 找到D中第一个与最大特征值相等的元素的位置，记录它的行和列
										% 注：find函数可以用来返回向量或者矩阵中不为0的元素的位置索引
disp('特征值法求权重的结果为：');
disp( V(:,c) ./ sum(V(:,c)) )           % 根据最大特征值的列数c，在V中找到对应的特征向量，再对此特征向量进行标准化
										% 标准化后的特征向量对应的就是各指标按照判断矩阵中一列的顺序对应的权重

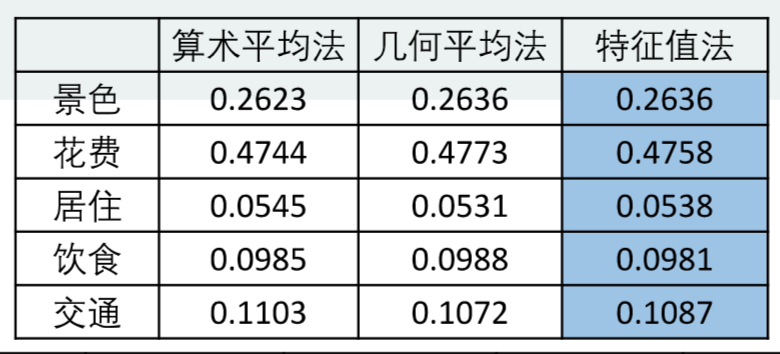
强烈建议三种方法都使用：

为了保证结果的稳健性，本文采用了三种方法分别求出了权重后计算平均值，再根据得到的权重矩阵计算个方案的得分，并进行排序和综合分析，这样避免了采用单一方法所产生的偏差，得出的结论更全面、更有效。

此步骤之后，就得到了准则层各指标对应的权重（选一种算法对应的一列即可）：

1.2.5 确定权重（方案层）

按照与准则层相同的步骤，确定方案层的权重：

按照确定准则层的标度，以同样的方式确定某个准则下方案层的标度，并得到该准则下的判断矩阵；
一致性检验；
计算权重——算术平均法、几何平均法、特征值法；

此步骤之后，就得到了方案层各方案在某一指标下对应的权重（可理解为该指标下的相对满意度）。

1.2.6 汇总结果并计算得分

将准则层权重和各准则下方案层的权重汇总，得到下表：

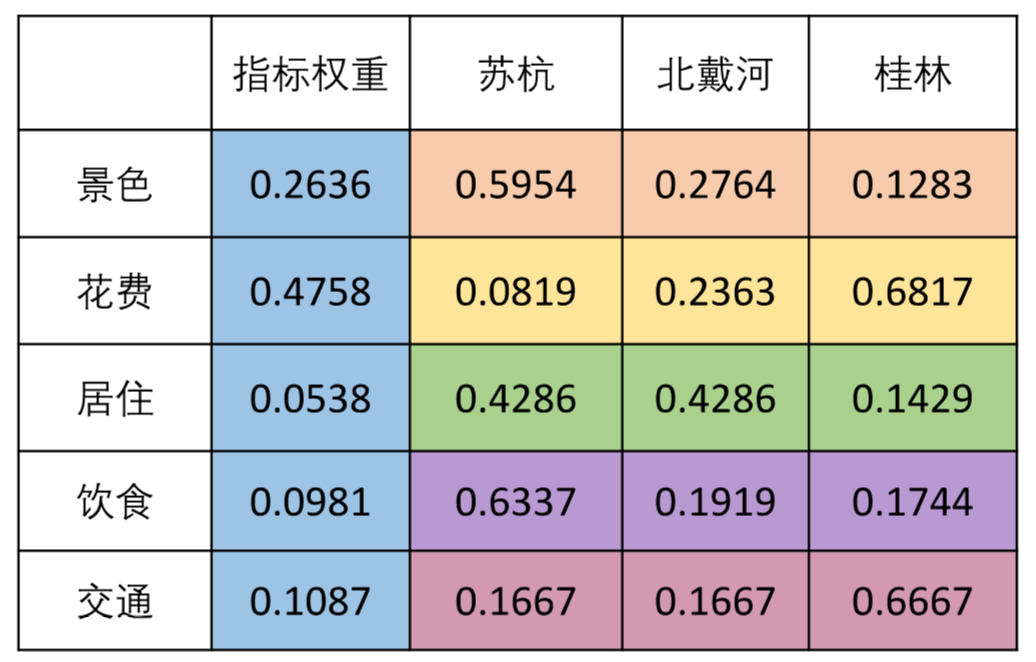
将各指标对应权重乘上某个方案在此指标下的权重并求和，得到该方案的得分。如：

类似可算出北戴河和桂林的得分。

1.3 模型拓展

待续

二、TOPSIS（优劣解距离法）

2.1 适用情况

准则层指标及方案层对应于准则层的权重已知，准则层指标的权重未知（多采用层次分析法求出）。

2.2 详细步骤

2.2.1 指标正向化

指标类型：

极大型指标：越大越好；
极小型指标：越小越好；
中间型指标：如 PH 值为 7 最好，越往两边越不好；
区间型指标：落在某个区间最好，如体温在 36~37℃ 最好；

指标正向化，即将各类指标转为极大型指标。

2.2.1.1 极小型指标

function [posit_x] = Min2Max(x)
    posit_x = max(x) - x;
    %posit_x = 1 ./ x;    %如果x全部都大于0，也可以这样正向化
end

2.2.1.2 中间型指标

function [posit_x] = Mid2Max(x,best)
    M = max(abs(x-best));                % 计算与标准数值间的距离
    posit_x = 1 - abs(x-best) / M;       % 按照极大型排列
end

2.2.1.3 区间型指标

function [posit_x] = Inter2Max(x,a,b)      % a为区间下界，b为区间上界
    r_x = size(x,1);                       % row of x 
    M = max([a-min(x),max(x)-b]);          % 区间与数值范围两端的距离
    posit_x = zeros(r_x,1);                % zeros函数用法: zeros(3)  zeros(3,1)  ones(3)
    % 初始化posit_x全为0  初始化的目的是节省处理时间
    for i = 1: r_x                         % 遍历每一行
        if x(i) < a                        % 如果低于下界
           posit_x(i) = 1-(a-x(i))/M;
        elseif x(i) > b                    % 如果高于上界
           posit_x(i) = 1-(x(i)-b)/M;
        else
           posit_x(i) = 1;                 % 界内为 1
        end
    end
end

2.2.1.4 完整代码

function [posit_x] = Positivization(x,type,i)
% 输入变量有三个：
% x：需要正向化处理的指标对应的原始列向量
% type： 指标的类型（1：极小型， 2：中间型， 3：区间型）
% i: 正在处理的是原始矩阵中的哪一列
% 输出变量posit_x表示：正向化后的列向量
    if type == 1  %极小型
        disp(['第' num2str(i) '列是极小型，正在正向化'] )
        posit_x = Min2Max(x);  %调用Min2Max函数来正向化
        disp(['第' num2str(i) '列极小型正向化处理完成'] )
        
    elseif type == 2  %中间型
        disp(['第' num2str(i) '列是中间型'] )
        best = input('请输入最佳的那一个值： ');
        posit_x = Mid2Max(x,best);
        disp(['第' num2str(i) '列中间型正向化处理完成'] )

    elseif type == 3  %区间型
        disp(['第' num2str(i) '列是区间型'] )
        a = input('请输入区间的下界： ');
        b = input('请输入区间的上界： '); 
        posit_x = Inter2Max(x,a,b);
        disp(['第' num2str(i) '列区间型正向化处理完成'] )

    else
        disp('没有这种类型的指标，请检查Type向量中是否有除了1、2、3之外的其他值')
    end
end

Position = input('请输入需要正向化处理的指标所在的列，例如第2、3、6三列需要处理，那么你需要输入[2,3,6]： '); 
disp('请输入需要处理的这些列的指标类型（1：极小型， 2：中间型， 3：区间型） ')
Type = input('例如：第2列是极小型，第3列是区间型，第6列是中间型，就输入[1,3,2]：  '); 
% 注意，Position和Type是两个同维度的行向量
for i = 1 : size(Position,2)  %这里需要对这些列分别处理，因此我们需要知道一共要处理的次数，即循环的次数
    X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));

2.2.2 标准化矩阵

2.2.2.1 不带权重的指标

Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);    % 求矩阵每一列元素的平方和，将平方和开方，并复制扩展n行
                                            % 用原矩阵每个元素除它所在列的平方和的开方
disp('标准化矩阵 Z = ')
disp(Z)

注：标准化方法不唯一，还可以为：x-x的均值/标准差，其主要目的是为了去除量纲的影响。

2.2.2.2 带权重的指标

可用层次分析法计算出每个指标的权重，详细请见本文的 “1.2.2 确定权重（准则层）”至 “1.2.4 计算权重（准则层）”。

但是层次分析法的主观性较强，更推荐使用熵权法进行修正。

2.2.3 计算得分并归一化

2.2.3.1 不考虑指标权重

代码实现：

D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ],2) .^ 0.5;  % D+ 与最大值的欧式距离向量；
													   % 相当于求出这个人的每项指标的成绩，和每项指标最高成绩的距离
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ],2) .^ 0.5;  % D- 与最小值的欧式距离向量；
S = D_N ./ (D_P+D_N);                                  % 未归一化的得分
stand_S = S / sum(S)                                   % 归一化得分
[sorted_S,index] = sort(stand_S ,'descend')            % 对矩阵各列降序排序，得到各列排序好的矩阵和索引矩阵；
                                                % 索引矩阵的每一列元素为对应排序后的矩阵每一列元素在原矩阵中的列索引

sort 举例：

2.2.3.2 考虑指标权重

注意：在计算得分时带上权重和在标准化矩阵中带上权重是几乎等效的，但是不可以在计算距离和标准化矩阵这两部都带上权重！（我这么想的，不知道对不对）

2.3 模型拓展

待续