美赛准备(3)

数模美赛赛前准备——插值与拟合

一、插值算法

1.1 适用场景与特点

1. 适用于数据量少的情况，用于补充数据以支持分析的进行；
2. 插值算法会计算出一个函数，这个函数经过所有已知样本点；
3. 一般在数据量大于30的时候就用拟合，小于30的时候就用插值；

1.2 多项式插值

1.2.1 多项式插值原理

对于 n+1 个互不相同的样本点，仅存在唯一的 n 阶多项式经过所有这些点；

注：个人认为，小于 n 阶的多项式是不能完全经过所有样本点的；但比 n 更高阶的多项式虽然可以经过所有点，它可能会产生一条振荡幅度很大的曲线（龙格现象）；

1.2.2 多项式插值方法

两种方法：拉格朗日插值、牛顿插值；

这两种插值都不能反映被插函数的性态（被插函数的性态需要在低阶和高阶的导数也保持一致性）

1.2.3 埃尔米特插值

效果：插值曲线在节点处是光滑的；

不但要求在节点的函数值相等，也要求导数值甚至高阶导数相等，但由于得到的多项式次数较高，也会出现龙格现象。

1.3 分段插值

1.3.1 分段三次埃尔米特插值

% 分段三次埃尔米特插值
x = -pi:pi; y = sin(x);   % -3.1416，-2.1416，  ... 2.8584
new_x = -pi:0.1:pi;       % 插值点
p = pchip(x,y,new_x);     % 输入样本点和插值点
figure(1);                % 在同一个脚本文件里面，要想画多个图，需要给每个图编号，否则只会显示最后一个图哦~
plot(x, y, 'o', new_x, p, 'r-')

1.3.2 三次样条插值

% 分段三次样条插值
x = -pi:pi; y = sin(x);   % -3.1416，-2.1416，  ... 2.8584
new_x = -pi:0.1:pi;       % 插值点
p = spline(x,y,new_x);    % 输入样本点和插值点
figure(2);                % 在同一个脚本文件里面，要想画多个图，需要给每个图编号，否则只会显示最后一个图哦~
plot(x, y, 'o', new_x, p, 'r-')

1.3.3 Matlab 画图

% plot函数用法:
% plot(x1,y1,x2,y2) 
% 线方式： - 实线 :点线 -. 虚点线 - - 波折线 
% 点方式： . 圆点  +加号  * 星号  x x形  o 小圆
% 颜色： y黄； r红； g绿； b蓝； w白； k黑； m紫； c青

% legend(string1,string2,string3, …)
% 分别将字符串1、字符串2、字符串3……标注到图中，每个字符串对应的图标为画图时的图标。
% ‘Location’用来指定标注显示的位置
% 如：legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast')   
% 上例标注显示在东南方向

%%%%%%%%%%%%%%%%%%%%%%%% 给x和y轴加上标签 %%%%%%%%%%%%%%%%%%%%%%%%%
xlabel('x的值')
ylabel('y的值')

%%%%%%%%%%%%%%%%%%%%%%% 图形显示配置 %%%%%%%%%%%%%%%%%%%%%%%
hold on % 继续在之前的图形上来画图形
grid on % 显示网格线

% %%%%%%%%%%%%%%%%%%%%%% 画出y=kx+b的函数图像 plot(x,y)  %%%%%%%%%%%%%%%%%%%%%%%%%%
% % 传统的画法：模拟生成x和y的序列，比如要画出[0,5]上的图形
% xx = 2.5: 0.1 :7  % 间隔设置的越小画出来的图形越准确
% yy = k * xx + b  % k和b都是已知值
% plot(xx,yy,'-')

% %%%%%%%%%%%%%%%%%%%%%%%%% 匿名函数的基本用法 %%%%%%%%%%%%%%%%%%%%%%%%%%
% handle = @(arglist) anonymous_function
% 其中handle为调用匿名函数时使用的名字。
% arglist为匿名函数的输入参数，可以是一个，也可以是多个，用逗号分隔。
% anonymous_function为匿名函数的表达式。
% 举个小例子
%  z=@(x,y) x^2+y^2; 
%  z(1,2) 
% % ans =  5
% fplot函数可用于画出匿名一元函数的图形。
% fplot(f,xinterval) 将匿名函数f在指定区间xinterval绘图。xinterval =  [xmin xmax] 表示定义域的范围
% 举个例子
f=@(x) k*x+b;
fplot(f,[2.5,7]);
legend('样本数据','拟合函数','location','SouthEast')

1.4 n维数据的插值

% n维数据的插值
% p = interpn(x1, x2, ...,xn, y, new_x1, new_x2,... ,new_xn, method)
% method:
% 'linear':线性插值（默认）；
% 'cubic'三次插值；
% 'spline'三次样条插值（最精准）；
% 'nearest'最邻近插值；

% 举个例子
x = -pi:pi; y = sin(x); 
new_x = -pi:0.1:pi;
p = interpn (x, y, new_x, 'spline');
% 等价于 p = spline(x, y, new_x);
figure(3);
plot(x, y, 'o', new_x, p, 'r-')

1.5 实操

1. 三次样条插值和三次埃尔米特插值都可以试一下，多项式插值一般用不到；
2. 插值算法可用于短期预测；
3. 表述：三次样条插值可以很好的保持数据的光滑性和连续性，减少信息量的损失。

二、拟合算法

1.1 插值和拟合的区别与选择

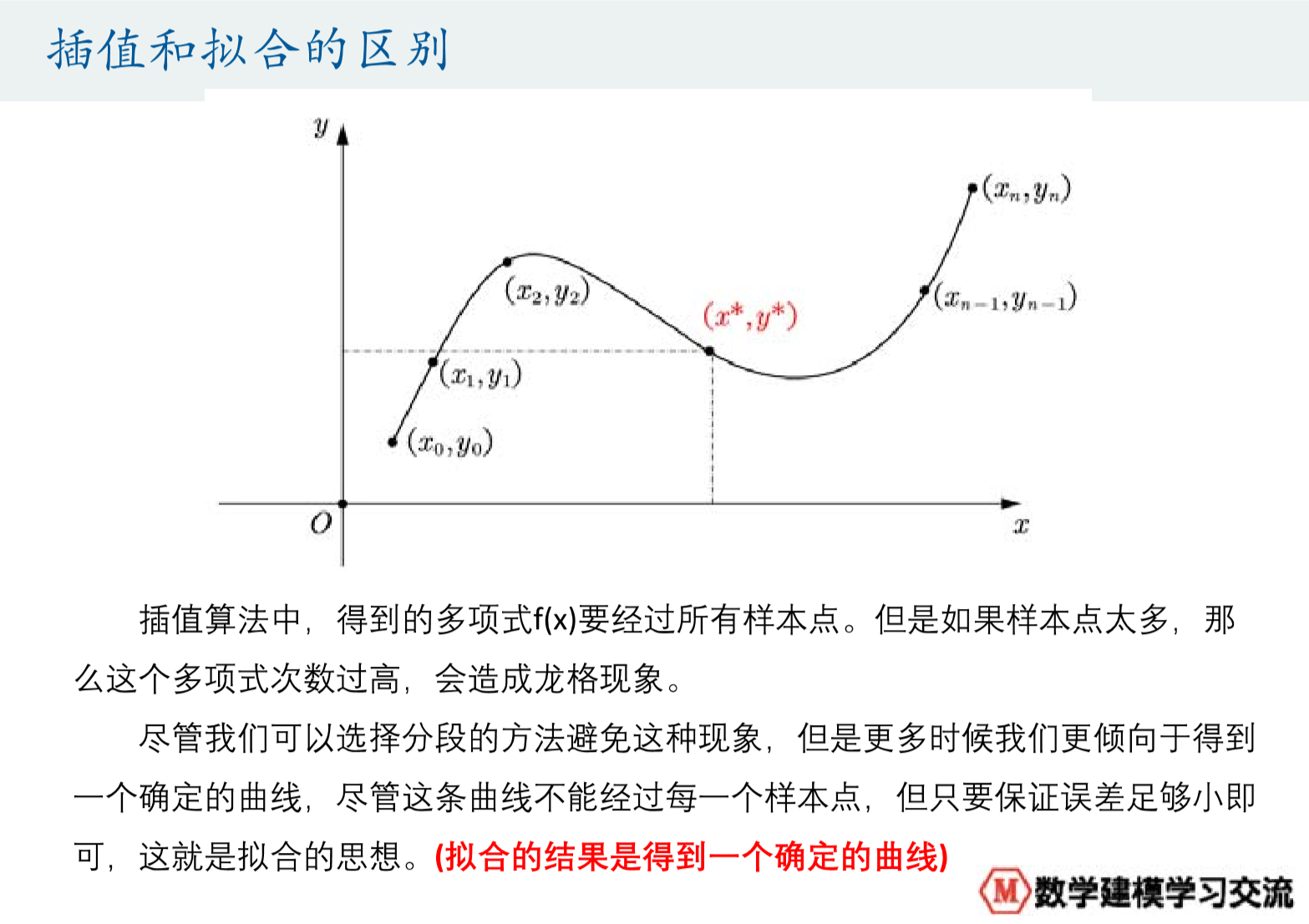
一般选择：当样本数量 > 30 时，可以认为这是一个大样本，可以选择拟合；当样本数量 < 30 时，需要进行插值。

1.2 拟合曲线的评价

注1：SST = SSE + SSR 仅对于拟合函数是线性函数时成立，因此拟合优度也只能评价线性拟合函数的好坏；

评价拟合函数的一般标准：

1. SSE 足够小；
2. 拟合函数形式足够简单；

y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2)  % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR   % 5.6843e-14  =   5.6843*10^-14   matlab浮点数计算的一个误差
R_2 = SSR / SST

注2：线性函数 指的是 对于参数线性，如下图：

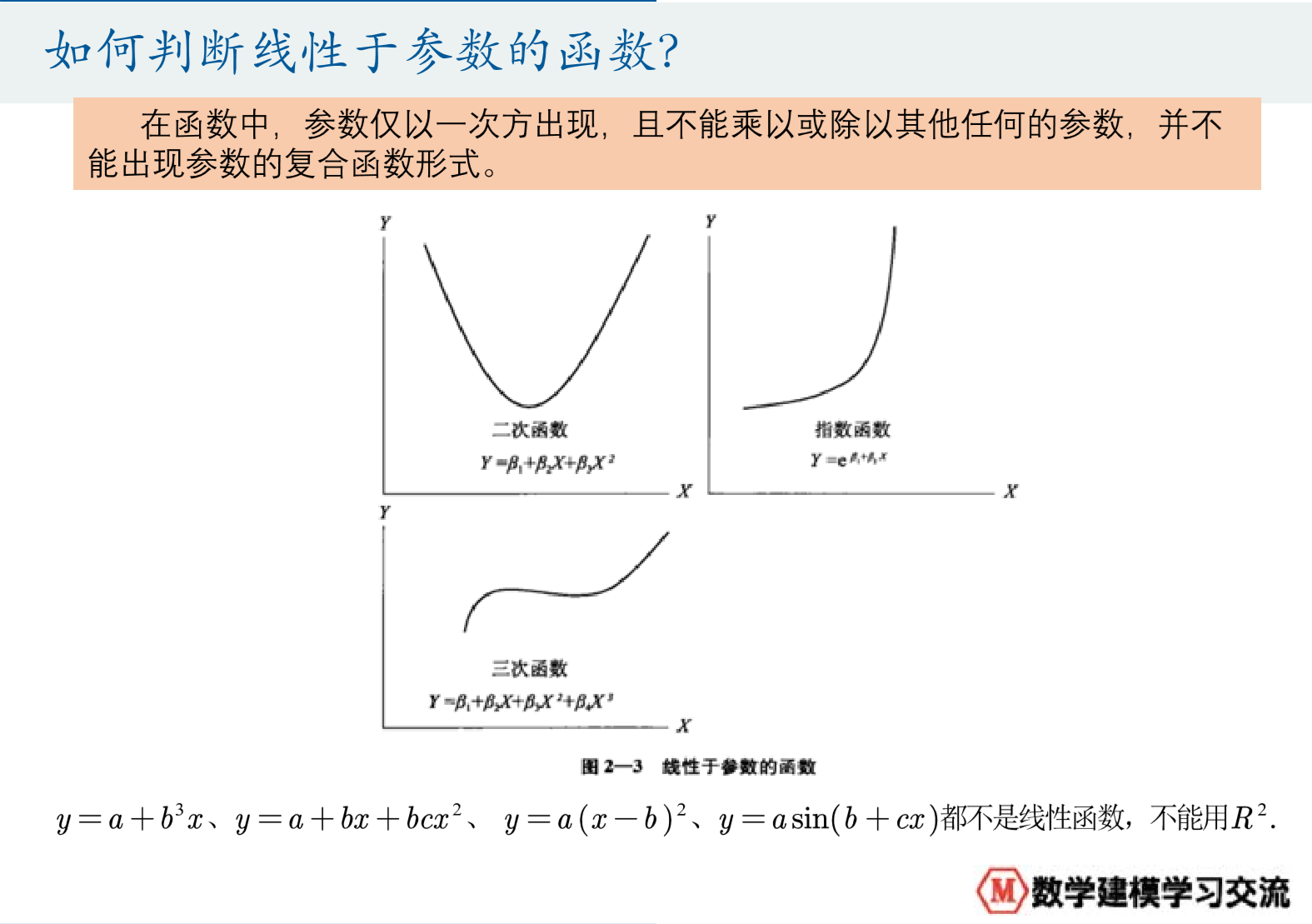
1.3 最小二乘法

clear;clc
load  data1
plot(x,y,'o')
% 给x和y轴加上标签
xlabel('x的值')
ylabel('y的值')
n = size(x,1);
k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))
hold on % 继续在之前的图形上来画图形
grid on % 显示网格线

1.4 拟合工具箱的使用

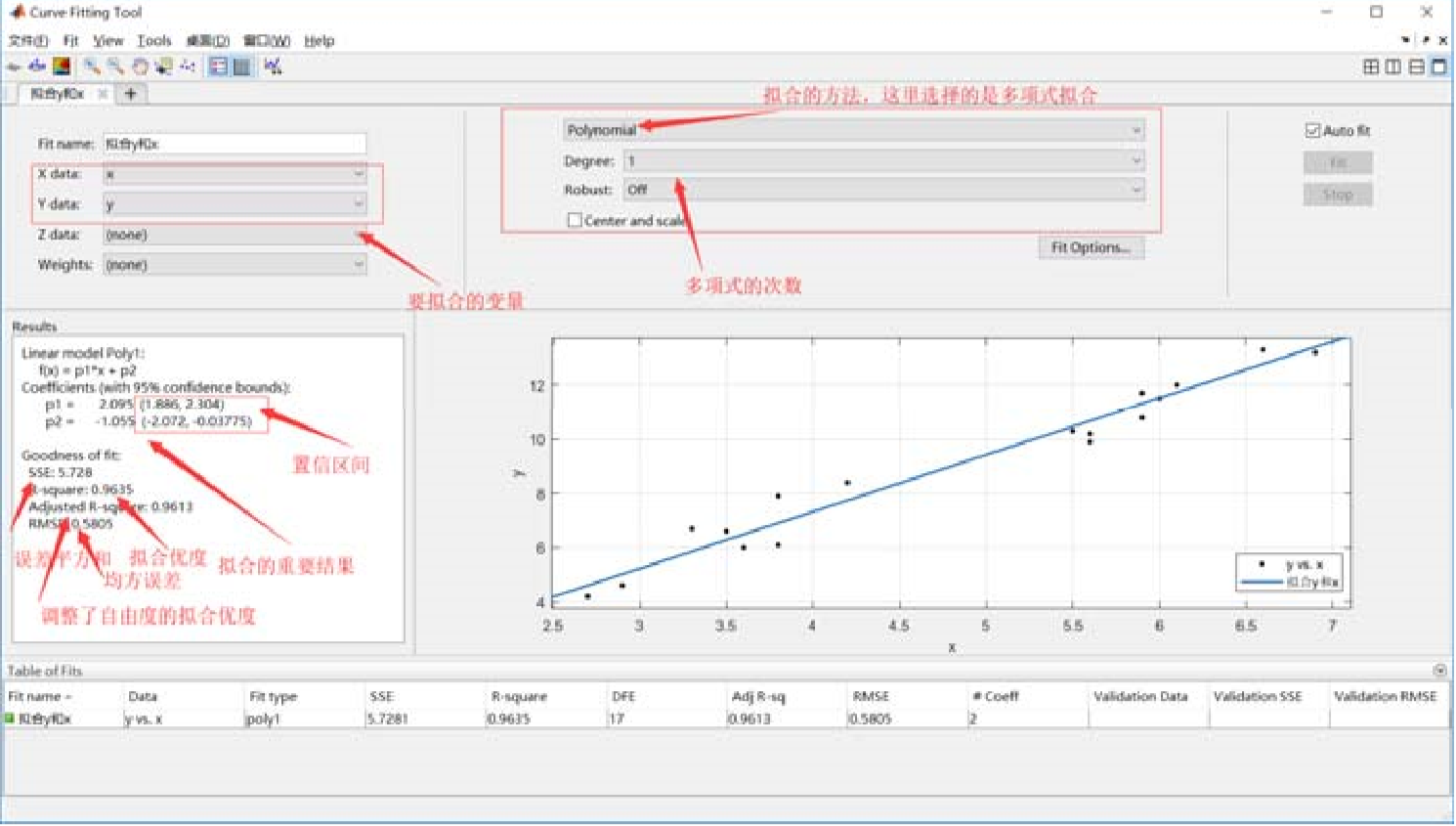
骚操作：可以用拟合工具箱 (cftool) 来绘三维函数图；

1.5 Matlab 生成随机数

% （1）randi : 产生均匀分布的随机整数（i = int）  
%产生一个1至10之间的随机整数矩阵，大小为2x5；
s1 = randi(10,2,5)
%产生一个-5至5之间的随机整数矩阵，大小为1x10；
s2 = randi([-5,5],1,10)

%  （2） rand: 产生0至1之间均匀分布的随机数
%产生一个0至1之间的随机矩阵，大小为1x5；
s3 = rand(1,5)
%产生一个a至b之间的随机矩阵，大小为1x5；  % a + (b-a) * rand(1,5); 如：a,b = 2,5
s4= 2 + (5-2) * rand(1,5)

% （3）normrnd:产生正态分布的随机数
%产生一个均值为0，标准差（方差开根号）为2的正态分布的随机矩阵，大小为3x4；
s5 = normrnd(0,2,3,4)

% （4）roundn—任意位置四舍五入
% 0个位 1十位  2百位 -1小数点后一位  
a = 3.1415
roundn(a,-2)    % ans   =  3.1400
roundn(a,2)      % ans   =  0
a =31415
roundn(a,2)   % ans  = 31400
roundn(5.5,0)  %6
roundn(5.5,1) %10

赏

谢谢你请我吃小鱼干